Solving the GCHQ Christmas Puzzle with Sentient
Follow @chrispatuzzoIntroduction
Last year, GCHQ, a British intelligence agency, set a Christmas puzzle comprised of a number of cryptic messages and convoluted problems for people to ponder. The first of these was a Nonogram. In this type of puzzle, the challenge is to shade a grid so that the numbers above and to the left of the grid correspond to consecutive runs of shaded cells. Here's the puzzle they set:
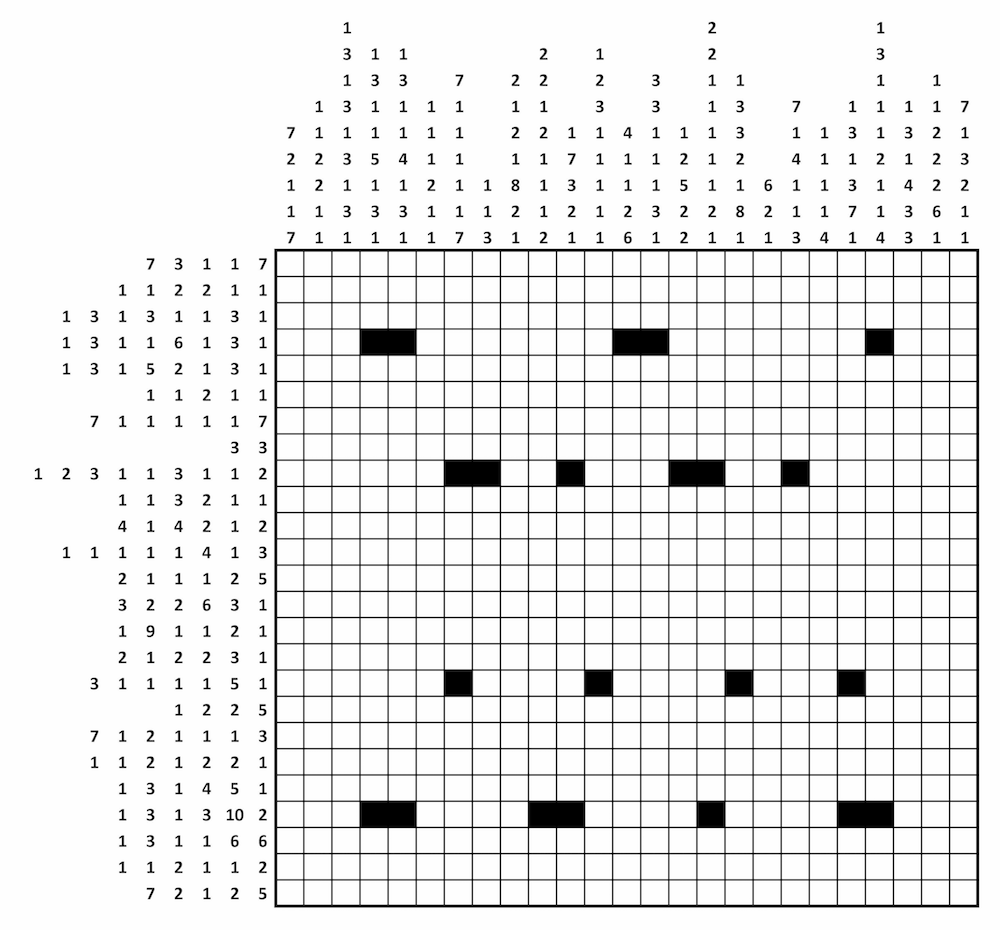
Nonograms are usually found in puzzle books and some are harder than others. It depends on how much information you are given at the start, as well as the amount of detail in the resulting image. If it has a lot of detail, there will be more numbers around the grid and this can help to derive the solution more quickly.
In this article I'm going to explain how to solve this puzzle with Sentient, which is an experimental programming language I've been writing. Sentient is "declarative" which means we only need describe the rules of the problem, nothing more. From this, Sentient can work backwards and solve this puzzle by itself.
Background
Before we dive in, let's elaborate what it means to "describe the rules of the problem":
Sentient programs are effectively descriptions of problems. These descriptions contain "invariants" which are things that must always be true for a solution to be valid. In our Nonogram puzzle, it is an invariant that the numbers around the grid correspond to its shaded cells. If they don't, it's not a correct Nonogram.
One way to think about Sentient programs are as solution checkers that check whether a given solution is correct or not. If someone presents you with an attempt at this puzzle, how would you check it? Well, you'd need to go through each of the numbers and verify that they do indeed correspond with the grid.
Unfortunately, the above two paragraphs are too ambiguous for Sentient. We'll need to be precise about what it means to check a puzzle and state its invariants clearly. Luckily, Sentient strives to be high-level and has a rich standard library that we can use to achieve this.
Getting Started
To get started, we're going to think about how we'd check a solution by hand. Let's consider the first row:

We need to look for seven shaded cells, followed by a gap, followed by three cells, another gap and so on. If we reach the end of the row and all numbers are accounted for then this row is valid. Here are three solutions:



Note that there can be an optional gap at the start of the row and one at the end (or both). As long as the shaded regions correspond to the numbers, the row is valid.
Surprisingly, there are 36 solutions for this row alone! Every shaded region must be delimited by a gap of at least one cell which means (7 + 3 + 1 + 1 + 7) + (5 - 1) = 23 cells are accounted for. That leaves a surplus of 2 gaps that can be placed in any one of (5 + 1) = 6 positions, which means there are 6^2 possibilities.
For our purposes, we don't actually care how many possibilities there are, so we'll move on.
Finite Bounds
Sentient programs must be finite in structure so we need to specify the dimensions of the grid as well as the maximum number of regions per row. The former is straightforward, we can just count how many cells are in the GCHQ puzzle and use that. This number can easily be changed later to cater for puzzles of different sizes.
To calculate the maximum number of regions per row, we should consider the worst case. If every region is of length one and there are no gaps at the start or end of the row, we get the following:

In general, this number will always be half the length of the row. If this is an odd number, we round up. In our case, the GCHQ puzzle is 25 cells across so we can set the number of regions to 13. If we wanted, we could just count the number of regions needed for the GCHQ puzzle, but this isn't very generic.
The Program
We're now ready to start writing our program! During this section, it may be useful to open the finished program side-by-side as reference. If the syntax doesn't make sense, don't worry– hopefully the descriptions following each code block will. Sentient's language syntax is documented here, but it's not a prerequisite.
First, let's declare a two-dimensional array of booleans to represent the grid. We'll use the convention that 'true' means the cell is shaded and 'false' means it is blank.
array25<array25<bool>> grid;
Next, we'll declare two more arrays. One for the numbers that go alongside the rows and the other for the numbers above the columns. As discussed earlier, each of these can contain up to 13 regions.
array25<array13<int6>> rowNumbers, columnNumbers;
You may be wondering where the 'int6' comes from. This is a type that supports integer values in the range -32 to 31. This will suffice because a single region cannot be bigger than the size of the grid, which is 25.
Currently, our arrays contain 13 numbers to represent regions, but 13 is an upper bound rather than the exact number of regions that must appear in each row. To cater for this, we'll invent the convention that the surplus regions are zero cells wide and remove them from our arrays before we use them.
function removeZeros (numbersArray) {
return numbersArray.map(function (numbers) {
return numbers.reject(*zero?);
});
};
The above function maps through an array of numbers and throws out elements that are zero. You can see that the standard library does most of the heavy lifting for us. We can now call this function on our row and column numbers. We'll re-assign these variables because we don't need to preserve the zero-width regions.
rowNumbers = removeZeros(rowNumbers);
columnNumbers = removeZeros(columnNumbers);
Now things get tricky! We need to somehow validate the grid is correct against these numbers. We looked at how to do this before, but for now, let's skip this conundrum and pretend we have a 'validate!' function that will check if the rows are correct. That lets us focus on finishing the body of our program at a high-level.
grid.validate!(rowNumbers);
To check the columns are correct, we can make excellent use of Sentient's 'transpose' function that swaps rows for columns in a two-dimensional array. This lets us re-use our 'validate!' function.
grid.transpose.validate!(columnNumbers);
Finally, the last thing we need to do is 'expose' the variables we're interested in. This makes sure the program prints out their values after it finishes running and allows us to set them as input.
expose grid, rowNumbers, columnNumbers;
And that concludes the high-level structure of our program. We haven't really captured what it means to check one of these puzzles yet, but at least we've got the basic structure in place.
Implementing 'validate!'
The 'validate!' function takes two parameters. The first is the 'grid', which is the target of the method call. The second is the set of row or column numbers to check. We've already standardised on rows by use of the 'transpose' method, so we only need to think about 'validate!' in terms of rows, which will be simpler.
function validate! (grid, rowNumbers) {
We need to check that each row of numbers corresponds to the grid. We'll start by iterating through and fetching the cells from the grid for that row.
rowNumbers.each(function^ (numbers, rowIndex) {
cells = grid[rowIndex];
The '^' modifier on the function allows it to 'reach outside' of its local scope and access the 'grid'. Next, we'll introduce three variables that we'll use to track the state of the row as we iterate over its cells.
previous = false;
count = 0;
index = -1;
The 'previous' variable will track whether the last cell we saw was shaded. The 'count' variable will track how many cells we've seen in the current region. The 'index' variable will track which region we are in from the set of numbers for the row. We haven't seen any cells yet, so we initialize 'previous' to 'false' and 'count' to '0'. We initialize 'index' to '-1' because arrays are 0-indexed and we're not in a region yet.
Next, we iterate through the cells for the current row of the grid.
cells.each(function^ (cell) {
We should only do something if we've reached an 'edge'. This is when the current cell differs from the previous cell. If the previous cell was shaded and this cell is blank, we're at an edge and vice versa.
edge = cell != previous;
More specifically, we should only do something if we've reached the end of a run of shaded cells. The gaps in the row can be as long as they like. It's only the shaded cells we care about. We're using the convention that shaded cells are 'true', so we've reached the end of a run if we're at an edge and the current cell is 'false'.
endOfRun = edge && !cell;
If it is the end of a run, we should increment our index as we are now in a region.
index += endOfRun ? 1 : 0;
We can now pull out the expected width of the region from the row numbers. We need to be a bit careful here because we might not be in a region yet, in which case, the index will be -1. By default, Sentient enforces that all indexes are within the bounds of the array. We can relax this by using the 'get' method rather than square brackets, which returns a second value which is whether the index is in bounds or not.
number, inBounds = numbers.get(index);
We can now enforce that if the current cell is the end of a run, the actual number of cells must be equal to the expected width from the row numbers. We do this with the 'invariant' keyword.
invariant endOfRun ? number == count : true;
If this isn't the end of a run, we don't want to enforce anything. An else clause of 'true' is a way to achieve this. Finally, if the current cell is an edge, we need to reset the count to '1' as we're now in a new region. Otherwise, we increment it. We also need to remember to set the 'previous' variable to the current cell for the next iteration.
count = edge ? 1 : count + 1;
previous = cell;
After we've scanned across the row, we need to add one final check that we've consumed all the numbers for the row. Otherwise, additional numbers would be ignored and the row could be deemed valid when it is not. For example, if the row had a single shaded cell and the numbers were 1, 9, 9, 9, this row would seem valid.
We can prevent this by adding an invariant after the iteration of each row.
invariant index == numbers.length - 1;
We've now reached the end of the 'validate!' method. We're so very close to finishing, but there's a small bug. If the row ends on a shaded cell, we're not currently enforcing anything about that region because that normally happens on the next iteration. We'll fix this (and do some refactoring!) in the next section.
Fixing the bug
Let's recap quickly: We've written a program that checks if the numbers alongside (and above) the grid correspond to its shaded cells. We do this by iterating through the cells in the grid one row or column at a time. We effectively 'tick off' numbers as we reach the end of shaded regions. We haven't yet dealt the case for when a row ends on a shaded cell because normally this 'ticking off' happens on the next available blank cell.
We can fix this relatively easily. If we reach the end of the row iteration and the previous cell was shaded, we should treat this as the end of a run and call the same code that increments the index and sets up the invariant.
index += previous ? 1 : 0;
number, inBounds = numbers.get(index);
invariant previous ? number == count : true;
In fact, we can extract this into a function and call this in both places. Again, we'll use the '^' modifier so we can access variables outside the local scope of the function. Naming this function is difficult. Let's name it after this 'ticking off' idea, which admittedly, is not a very good one.
function^ tickOffNumberIf (condition) {
index += condition ? 1 : 0;
number, inBounds = numbers.get(index);
invariant condition ? number == count : true;
};
We can now call this in two places. One inside the loop and the second after it finishes.
# Inside the loop:
tickOffNumberIf(endOfRun);
# After it finishes:
tickOffNumberIf(previous);
Finished program
Below is the program in its entirety. The high-level code is wrapped in a 'main' function, although it doesn't need to be. This lets us place the high-level code at the top rather than after the other function definitions.
function main () {
array25<array25<bool>> grid;
array25<array13<int6>> rowNumbers, columnNumbers;
rowNumbers = removeZeros(rowNumbers);
columnNumbers = removeZeros(columnNumbers);
grid.validate!(rowNumbers);
grid.transpose.validate!(columnNumbers);
expose grid, rowNumbers, columnNumbers;
};
function removeZeros (numbersArray) {
return numbersArray.map(function (numbers) {
return numbers.reject(*zero?);
});
};
function validate! (grid, rowNumbers) {
rowNumbers.each(function^ (numbers, rowIndex) {
cells = grid[rowIndex];
previous = false;
count = 0;
index = -1;
cells.each(function^ (cell) {
edge = cell != previous;
endOfRun = edge && !cell;
tickOffNumberIf(endOfRun);
count = edge ? 1 : count + 1;
previous = cell;
});
tickOffNumberIf(previous);
invariant index == numbers.length - 1;
});
};
function^ tickOffNumberIf (condition) {
index += condition ? 1 : 0;
number, inBounds = numbers.get(index);
invariant condition ? number == count : true;
};
main();
The whole thing comes in at 49 lines, which doesn't seem too bad. Notice that we've kept true to our word and haven't told Sentient how to solve this problem. We've defined how to check a solution if given one. To run this program, we first need to compile it. We'll also use Sentient's optimiser to speed things up.
$ sentient --compile --optimise nonogram.snt > nonogram.json
This takes about 90 seconds on my laptop and produces a 23MB program. We now have a generic Nonogram program that we can use to solve any puzzle of size 25. The last thing to do is to plug in the numbers for the GCHQ puzzle. We can use the '--assign-file' command-line option to pass in some JSON.
$ sentient --run nonogram.json --assign-file gchq.json
Here's the GCHQ puzzle transcribed (by hand!) to JSON. The full version is here.
{
"rowNumbers": [
[7, 3, 1, 1, 7],
[1, 1, 2, 2, 1, 1],
[1, 3, 1, 3, 1, 1, 3, 1],
// ...
],
"columnNumbers": [
[7, 2, 1, 1, 7],
[1, 1, 2, 2, 1, 1],
[1, 3, 1, 3, 1, 3, 1, 3, 1],
// ...
],
"grid": {
"3": {
"3": true, "4": true,
"12": true, "13": true,
"21": true
},
"8": {
"6": true, "7": true,
"10": true,
"14": true, "15": true,
"18": true
},
// ...
}
}
Sentient solves this problem in about 7 seconds and produces the following output.
{"grid":[[true,true,true,true,true,true,true,false,true,true,true,false,false,false,true,false,true,false,true,true,true,true,true,true,true],[true,false,false,false,false,false,true,false,true,true,false,true,true,false,false,false,false,false,true,false,false,false,false,false,true],[true,false,true,true,true,false,true,false,false,false,false,false,true,true,true,false,true,false,true,false,true,true,true,false,true],[true,false,true,true,true,false,true,false,true,false,false,true,true,true,true,true,true,false,true,false,true,true,true,false,true],[true,false,true,true,true,false,true,false,false,true,true,true,true,true,false,true,true,false,true,false,true,true,true,false,true],[true,false,false,false,false,false,true,false,false,true,true,false,false,false,false,false,false,false,true,false,false,false,false,false,true],[true,true,true,true,true,true,true,false,true,false,true,false,true,false,true,false,true,false,true,true,true,true,true,true,true],[false,false,false,false,false,false,false,false,true,true,true,false,false,false,true,true,true,false,false,false,false,false,false,false,false],[true,false,true,true,false,true,true,true,false,false,true,false,true,false,true,true,true,false,true,false,false,true,false,true,true],[true,false,true,false,false,false,false,false,false,true,true,true,false,true,true,false,false,false,false,true,false,false,false,true,false],[false,true,true,true,true,false,true,false,true,true,true,true,false,true,true,false,true,false,false,false,false,true,true,false,false],[false,true,false,true,false,false,false,true,false,false,false,true,false,true,false,true,true,true,true,false,true,false,true,true,true],[false,false,true,true,false,false,true,false,true,false,true,false,false,false,false,false,false,true,true,false,true,true,true,true,true],[false,false,false,true,true,true,false,true,true,false,true,true,false,true,true,true,true,true,true,false,true,true,true,false,true],[true,false,true,true,true,true,true,true,true,true,true,false,true,false,true,false,false,true,true,false,false,false,false,true,false],[false,true,true,false,true,false,false,true,true,false,false,false,true,true,false,true,true,true,false,false,false,false,false,true,false],[true,true,true,false,true,false,true,false,true,false,false,true,false,false,false,false,true,true,true,true,true,false,true,false,false],[false,false,false,false,false,false,false,false,true,false,false,false,true,true,false,true,true,false,false,false,true,true,true,true,true],[true,true,true,true,true,true,true,false,true,false,false,true,true,false,false,false,true,false,true,false,true,false,true,true,true],[true,false,false,false,false,false,true,false,true,true,false,false,true,false,false,true,true,false,false,false,true,true,false,true,false],[true,false,true,true,true,false,true,false,false,false,true,true,true,true,false,false,true,true,true,true,true,false,false,true,false],[true,false,true,true,true,false,true,false,true,true,true,false,true,true,true,true,true,true,true,true,true,true,false,true,true],[true,false,true,true,true,false,true,false,true,false,false,true,true,true,true,true,true,false,true,true,true,true,true,true,false],[true,false,false,false,false,false,true,false,false,true,true,false,false,false,false,false,false,true,false,true,false,true,true,false,false],[true,true,true,true,true,true,true,false,true,true,false,false,false,true,false,true,true,false,false,false,true,true,true,true,true]],"rowNumbers":[[7,3,1,1,7],[1,1,2,2,1,1],[1,3,1,3,1,1,3,1],[1,3,1,1,6,1,3,1],[1,3,1,5,2,1,3,1],[1,1,2,1,1],[7,1,1,1,1,1,7],[3,3],[1,2,3,1,1,3,1,1,2],[1,1,3,2,1,1],[4,1,4,2,1,2],[1,1,1,1,1,4,1,3],[2,1,1,1,2,5],[3,2,2,6,3,1],[1,9,1,1,2,1],[2,1,2,2,3,1],[3,1,1,1,1,5,1],[1,2,2,5],[7,1,2,1,1,1,3],[1,1,2,1,2,2,1],[1,3,1,4,5,1],[1,3,1,3,10,2],[1,3,1,1,6,6],[1,1,2,1,1,2],[7,2,1,2,5]],"columnNumbers":[[7,2,1,1,7],[1,1,2,2,1,1],[1,3,1,3,1,3,1,3,1],[1,3,1,1,5,1,3,1],[1,3,1,1,4,1,3,1],[1,1,1,2,1,1],[7,1,1,1,1,1,7],[1,1,3],[2,1,2,1,8,2,1],[2,2,1,2,1,1,1,2],[1,7,3,2,1],[1,2,3,1,1,1,1,1],[4,1,1,2,6],[3,3,1,1,1,3,1],[1,2,5,2,2],[2,2,1,1,1,1,1,2,1],[1,3,3,2,1,8,1],[6,2,1],[7,1,4,1,1,3],[1,1,1,1,4],[1,3,1,3,7,1],[1,3,1,1,1,2,1,1,4],[1,3,1,4,3,3],[1,1,2,2,2,6,1],[7,1,3,2,1,1]]}
The output isn't readable in this form, so I cobbled together some Ruby to turn it into an image. Here it is.

As you can see, this is a QR code. It links to the rest of the puzzles in the series. How delightful!
Closing words
If you've got this far, well done for following along. Hopefully you can see that Sentient is a viable tool for solving certain kinds of problem. There may be faster methods available, but would they be faster to write? Sentient programs try to reflect how programmers actually think about the problems they solve. The language is an experiment into power of expression and the translation of an idea into code.
By capturing the essence of the Nonogram problem through a program that checks a solution, we've created a program that can solve this problem. This may seem counter-intuitive. The world doesn't normally work this way. Knowing what great coffee tastes like doesn't automatically mean we're able to brew great coffee.
If you're interested in Sentient and want to learn more, check out sentient-lang.org.